It was a Monday. I was 14, and my math tuition class was in 2 hours. I was hurriedly going through the homework to be done. Yes, we’re all major procrastinators. My tutor had given 12 questions on division by integers. It was always 12 questions, because he could divide that number in many ways. This was useful in formatting the page layout of the questions; 2, 3, or even 4 columns per row.
It was basic arithmetic, and there were two or three questions with 7 as the denominator. I don’t remember exactly what the numbers were, so let’s say they were 1/7, 2/7, and 5/7. Then there were other fractions with 3, 11, 5 and so on. While working out the decimal representations of these numbers, I realized something – the decimal part of fractions with 7 as the denominator had the same set of numbers, recurring every 6 digits.

As you can see above, the numbers 1, 2, 4, 5, 7, and 8 repeat in the decimal part of these rational numbers. Interestingly, they repeat in a manner that shows a cyclic rotation; 142857 is repeated such that n/7 starts from the nth largest number in the sequence 1, 4, 2, 8, 5, and 7, rolling over to the beginning when it reaches the end of the sequence.
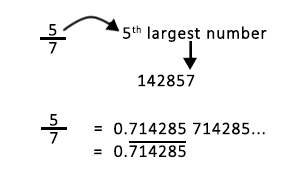
This means we can figure out the decimals of a number divided by seven, just by remembering the number 142857. Don’t ask me who would remember a random number like that. Some of us just do.
For example, let’s take 213/7. Looking at the numerator, one could figure out that 210 is the nearest number divisible by 7. (21 = 3 x 7. Multiplication tables, anyone?). That means the decimal representation is 30… something, as the remainder is 3. For the decimal part, we have 30 + 3/7, where 3/7 is 0.428571… by the above pattern. So the answer for 213/7 = 30.428571…
Pretty neat, as long as you remember 142857.
That’s not all. Many rational numbers have recurring patterns in their decimal part. For example, any number divided by 9 gives the same number. So 4/9 = 0.444444… and 7/9 = 0.77777….
Similarly, division by 11 results in multiplying the numerator by 9, and representing it to two decimal points, which then repeats itself. Thus,
5/11 = 0.45 45 45… where 45 = 5 x 9
3/11 = 0.27 27 27 … where 27 = 3 x 9 .
Naturally, I was curious whether other numbers showed the same behaviour as 7. So I checked the decimal part of different rational numbers, intuitively checking with prime numbers as the denominator, since 7 is prime. I didn’t make much progress there, but I remember realizing 17 had such a cyclic rotation in its fractions. I just couldn’t figure out an easy way to derive the starting point of the repetend. Not that it would have been very useful anyway – the length of the repetend of 1/p is either p-1, or a factor of p-1 – not that easy to remember. I’ve only tried a max of 16 digits to remember in order so far. You can probably guess what for.
Looking back now, I had accidentally discovered Cyclic Numbers. It was fun to play around with numbers back then, and we had enough free time to do stuff like that. Some of the best days, those were. And not just because of arithmetics ?
If you’re interested in learning more about Repeating Decimals and Cyclic Numbers, take a look at the following Wikipedia articles. Have fun!
